A hash table is data structure that is used to search for exact matches to a search key. For searching, they work like this:
- Take a search key (example: the word “cat”)
- Hash the search key: pass the key to a function that returns an integer value (example: the hash function returns 47 when the input key is “cat”)
- Use the integer value to inspect a slot to see if it contains the search key (example: look in an array at element 47)
- If the key matches, great, you’ve found what you’re looking for and you can retrieve whatever metadata you’re looking for (example: in array element 47, we’re found the word “cat”. We retrieve metadata that tells us “cat” is an “animal”)
- If the key doesn’t match and the slot contains something besides the key, carry out a secondary search process to make sure the search key really isn’t stored in the hash table; the secondary search process varies depending on the type of hashing algorithm used (example: in array element 47, we found the word “dog”. So, let’s look in slot 48 and see if “cat” is there. Slot 48 is empty, so “cat” isn’t in the hash table. This is called linear probing, it’s one kind of secondary search)
I had a minor obsession with hash tables for ten years.
The worst case is terrible
Engineers irrationally avoid hash tables because of the worst-case O(n) search time. In practice, that means they’re worried that everything they search for will hash to the same value; for example, imagine hashing every word in the English dictionary, and the hash function always returning 47. Put differently, if the hash function doesn’t do a good job of randomly distributing search keys throughout the hash table, the searching will become scanning instead.
This doesn’t happen in practice. At least, it won’t happen if you make a reasonable attempt to design a hash function using some knowledge of the search keys. Indeed, hashing is usually in the average case much closer to O(1). In practice, that means almost always you’ll find what you’re looking for on the first search attempt (and you will do very little secondary searching).
Hash tables become full, and bad things happen
The story goes like this: you’ve created a hash table with one million slots. Let’s say it’s an array. What happens when you try and insert the 1,000,001st item? Bad things: your hash function points you to a slot, it’s full, so you look in another slot, it’s full, and this never ends — you’re stuck in an infinite loop. The function never returns, CPU goes through the roof, your server stops responding, and you take down the whole of _LARGE_INTERNET_COMPANY.
This shouldn’t happen if you’ve spent time on design.
Here’s one solve: there’s a class of hash tables that deal with becoming full. They work like this: when the table becomes x% full, you create a new hash table that is (say) double the size, and move all the data into the new hash table by rehashing all of the elements that are stored in it. The downside is you have to rehash all the values, which is an O(n) [aka linear, scanning, time consuming] process.
Here’s another solve: instead of storing the metadata in the array, make your array elements pointers to a linked list of nodes that contain the metadata. That way, your hash table can never get full. You search for an element, and then traverse the linked list looking for a match; traversing the linked list is your secondary hash function. Here’s a diagram that shows a so-called chained hash table:
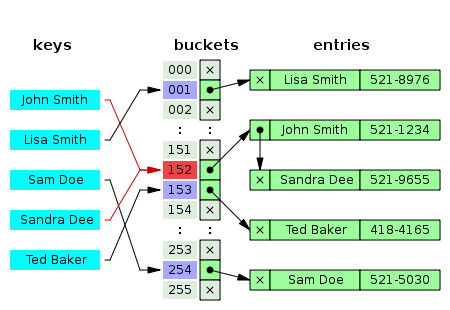
A chained hash table, showing “John Smith” and “Sandra Dee” both in slot 152 of the hash table. You can see that they’re chained together in a linked list. Taken from Wikipedia, http://en.wikipedia.org/wiki/Hash_table
Chained hash tables are a very good idea. Problem solved.
By the way, I recommend you create a hash table that’s about twice the size of the number of elements you expect to put into the table. So, suppose you’re planning on putting one million items in the table, go ahead and create a table with two million slots.
Trees are better
In general, trees aren’t faster for searching for exact matches. They’re slower, and here’s peer-reviewed evidence that compares B-trees, splay trees, and hashing for a variety of string types. So, why use a tree at all? Trees are good for inexact matches — say finding all names that begin with “B” — and that’s a task that hash tables can’t do.
Hash functions are slow
I’ve just pointed you to research that shows that must not be true. But there is something to watch out for: don’t use the traditional modulo based hash function you’ll find in your algorithms text book; for example, here’s Sedgewick’s version, note the “% M” modulo operation that’s performed once per character in the input string. The modulo is used to ensure that the hash value falls within the size of the hash table — for example, if we have 100 slots and the hash function returns 147, the modulo turns that into 47. Instead, do the modulo once, just before you return from the hash function.
Here’s the hash function I used in much of my research on hashing. You can download the code here.

A very fast hash function written in C. This uses bit shifts, and a single modulo at the end of the function. If you find a faster one, would love to hear about it.
Hash tables use too much memory
Again, not true. The same peer-reviewed evidence shows that a hash table uses about the same memory as an efficiently implemented tree structure. Remember that if you’re creating an array for a chained hash table, you’re just creating an array of pointers — you don’t really start using significant space until you’re inserting nodes into the linked lists that are chained from the hash table (and those nodes typically take less space than nodes in a tree, since they only have one pointer).
One Small Trick
If you want your hash tables to really fly for searching, move any node that matches your search to the front of the chained list that it’s in. Here’s more peer-reviewed evidence that shows this works great.
Alright. Viva Hash Tables! See you next time.